

Next: CSDP
Up: The Codes
Previous: SDPA
Author: Sturm
Version: 1.04, 9/2000;
Available: yes, from http://fewcal.kub.nl/sturm/software/sedumi.html
Key papers: [24,25]
Features: self-dual embedding, dense column handling
Language, Input format: Matlab+C; Matlab, SDPA, SDPpack
Error computations: yes
Solves: SDP/SOCP
The primal-dual interior point algorithm implemented in
SeDuMi [24] is described in [25]. The algorithm
has an
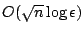 worst case bound, and treats
initialization issues by means of the self-dual embedding technique of
[28]. The iterative solutions are updated in a product
form, which makes it possible to provide highly accurate solutions.
worst case bound, and treats
initialization issues by means of the self-dual embedding technique of
[28]. The iterative solutions are updated in a product
form, which makes it possible to provide highly accurate solutions.
The algorithm terminates successfully if the norm of the residuals in
the optimality conditions, or the Farkas system with 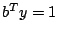 or
or
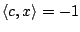 , are less than the parameter pars.eps. The default
value for pars.eps is 1E-9.
, are less than the parameter pars.eps. The default
value for pars.eps is 1E-9.
Remarks:
- SeDuMi exploits sparsity in
solving the normal equations; this results in a benefit for problems
with a large number of small order matrix variables, such as the copositivity-problems in the Dimacs set.
- However, for problems that
involve a huge matrix variable (without a block diagonal structure),
the implementation is slow and consumes an excessive amount of memory.
Hans D. Mittelmann
2002-08-17
![]() worst case bound, and treats
initialization issues by means of the self-dual embedding technique of
[28]. The iterative solutions are updated in a product
form, which makes it possible to provide highly accurate solutions.
worst case bound, and treats
initialization issues by means of the self-dual embedding technique of
[28]. The iterative solutions are updated in a product
form, which makes it possible to provide highly accurate solutions.
![]() or
or
![]() , are less than the parameter pars.eps. The default
value for pars.eps is 1E-9.
, are less than the parameter pars.eps. The default
value for pars.eps is 1E-9.